Term Paper.
Choose topic by March 26.
Written text due April 29.

Oral presentations on May 2, 3, & 6.

 

·         These are just suggestions of topics for your term paper. Pick one, or propose one yourself, and tell me your choice by March 26, 2002.

·         The paper should be 6 - 10 pages long. Use at least two other sources than Serway. Illustrative calculations, examples, and figures are urged.

·         Due,  April 29, 2002. Class presentations of 30 minutes length will be given on May 2, 6, and May 8.

 

·         Quantum Statistics

 

Explain black-body radiation and the Einstein theory of heat capacity of solids.  First treat the ``ultra-violet catastrophe'' in the context of black-body radiation and the rule of Delong and Petit in the context of heat capacity. You will need to understand basics of classical statistical mechanics, such as the Boltzmann distribution. Then you will need to learn some quantum statistics. Many books (including ours) treat this material. Give some examples of black-body radiation. Find spectra for the sun and compare with black body radiation. What temperature should the earth be if it acts as a black-body and absorbs all of the energy she receives from the sun? Another important example to discuss is the 3 degree cosmic microwave background. Modern Physics by Krane has a discussion of this material in chap. 16. Also see the cosmology assignment below. Finally, calculate the heat capacity of a ``photon gas''.

 

·         Cosmology

 

Read Steven Wienberg's The First Three Minutes (one of the best popular physics book I have read) and chap 16 of Modern Physics by Krane and write a paper summarizing this material. Krane has a good synopsis of Wienberg's book and touches on the main points through the moment of decoupling of matter and radiation. Maybe explore one topic not covered in Wienberg - such as the concept of inflation.

 

·         Nucleosynthesis

 

Describe how the elements are synthesized out of protons. What is the abundance of elements on earth? In the universe? In our sun? Discuss the "binding curve'' or energy per nucleon. Why is energy released if nuclei with total mass number less than Iron fuse? Why is energy released is nuclei with mass number greater than Iron undergo fission? Discuss stellar evolution, proton-proton chain, the CNO cycle, r and s processes, Solar neutrino experiments, the end points of stars such as supernovae, white dwarfs, neutron stars, black holes. Chaps 12, 13, and 15 of Modern Physics by Krane also contains pertinent information. You will need to consult some outside sources as well. I like the book The Physical Universe: An Introduction to Astronomy,  F. H. Shu.

 

·         Elementary Particles

 

Chap 15 of Serway has an intro to particle physics, as does Chap 14 of Modern Physics by Krane. Describe the families of particles. How do they interact? What conservation laws are obeyed? What is the pion model for the nuclear force? Describe the quark model and the standard model.  What is confinement? What is beta decay and the weak interaction? What implications for particle physics does the decay of the proton have?  Discuss the recent evidence that quarks may have substructure (Phys. Rev. Lett - 96). What are the features of the accelerators used to study subatomic particles? the detectors? References on the quark model are given in chap. 15 of Modern Physics by Serway. Discuss the standard model in the context of the chapter Beautiful Theories in Weinberg's book In Search for the Final Theory.

 

 

·         Chemistry

 

Discuss orbitals in atoms. Describe the properties of the elements, like atomic radii, electronegativity, and ionization energy in terms of the shell model. Describe different types of bonds - hydrogen bonding, ionic, and covalent bonds. Describe the various excitations of bond molecules - rotational and vibrational excitations. How are they measured? What are the spectra? Our book touches on many of these topics. Pauling, The Chemical Bond and Herzberg, Molecular Spectra and Molecular Structure are good. These and other references are given in Krane.

 

·         Diodes and Transistors


Discuss conductivity in metals and semiconductors in terms of conduction bands and band gaps. This material is covered in chap. 11 of Serway. Describe "holes" and  "doping". Describe the various diodes, zener, tunnel, light-emitting (LED). You will need to learn some QM statistical physics - the Fermi-Dirac distribution and the Maxwell distribution, treated in chap. 9 of Serway. Try to understand and explain transistors (much harder). If you are ambitious, you can treat semi-conductor lasers. The solid-state textbooks by Kittel or Ashcroft and Mermin are good sources.

 

·         Theory of Everything. 

 

Steven Weinberg: Dreams of a Final Theory. An extremely well written book  by the Nobel laureate who unified three of the four forces. Discusses authors view that high energy theory is the most fundamental possible theory.

 

·         String theory.  

 

Read  the book on string theory by Michio Kaku: Hyperspace : a scientific odyssey through parallel universes, time warps, and the tenth dimension. New York : Oxford University Press, 1994. It is in the science library. I haven’t read it, but heard it was good.

 

Or read the book by Brian Green: The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory. This is a very well written book.

 

 

 

Stephen W. Hawking,  A brief history of time  York : Bantam Books, 1998. In our library. What is a black hole. Discuss entropy of black holes. Hawking radiation. Well written book by leader in quantum gravity.

 

 

Read a book by Prof. Schweber (of the Brandeis history and physics departments). Either one on the history of Quantum Electrodynamics: "QED and the Men Who Made It: Dyson, Feynman, Schwinger, and Tomonaga", Silvan S. Schweber, Princeton University Press, 1994. Or one on Robert Oppenheimer: "In the Shadow of the Bomb", Silvan S. Schweber, Princeton University Press, 2000.

 

 

Review the technology and politics of fission energy. Concentrate on the new pebble reactors. See articles in Scientific American (Next-Generation Nuclear Power, January 2002; by James A. Lake, Ralph G. Bennett and John F. Kotek.) Scientific American is available on-line. Here is a link to other articles from web searches.

 

 

·         Band theory and the Kronig-Penny model

 

``Electrons moving in a metal experience a periodic potential from the positive nucleus of the atoms arranged on the crystalline lattice. As a consequence, the energy spectrum of the electrons consists of continuous bands separated by forbidden gaps. The band structure of the energy levels of electrons in a periodic lattice is a direct consequence of the wave nature of matter. It is essential to an understanding of many basic properties of the solid state of matter and indispensable in the quantum theory of electric conduction in metals. Even in its crudest and most schematic form it accounts qualitatively for the distinction between conductors and insulators. In its refined form the band theory is able to correlate a large amount of experimental data quantitatively. In applications to the solid state, quantum mechanics has scored some of its greatest triumphs.''  -          Merzbacher - Quantum Mechanics

 

Model the potential seen by an electron in a metal as a 1-dimensional periodic array of rectangular barriers. Calculate the transmission matrix P for a particle to cross the well.

 

The solution to the Schrodinger eq. for a single square barrier is

 

 

the boundary conditions of continuity of the wave function and its derivative set linear relations between the coefficients so that

with P a matrix.

  

 

 


 

 

 

 

 

 

Consider the barriers to exist on a closed ring of N barriers. On the periodic closed circle the wave function has the condition that  In other words, the wave function is periodic. In terms of the matrix solution or PN = 1.

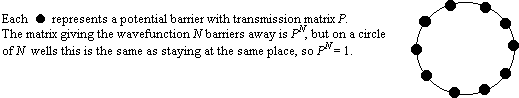Find the matrix P and find what energies satisfy the relation PN = 1 as a function of N. You will find that the allowed energies cluster into bands of energies merging into a continuum with gaps between bands. This method of solving for the energy spectrum of a periodic potential is based on a scattering approach. It is discussed fully in the QM book by Merzbacher. Examine Solid State textbooks by Ashcroft and Mermin or Kittel to find the solution based on solving the Schrodinger equation. Our book discusses this material in chap. 9. Modern Physics by Krane also has a section on this material in chap 11.